밑바닥부터 시작하는 딥러닝 - 게이트가 추가된 RNN(2)

카테고리 없음

밑바닥부터 시작하는 딥러닝 - 게이트가 추가된 RNN(2)

Leesemo 2021. 10. 30. 15:15

기울기 소실과 LSTM

LSTM의 인터페이스

위의 그림은 계산 그래프를 단순화하는 도법이다. 행렬 계산 등을 하나의 직사각형 노드로 정리해 그리는 방식이다.

tanh 계산으로 직사각형 노드를 하나 그린다. 이 직사각형 노드 안에 행렬 곱과 편향의 합, 그리고 tanh 함수에 의한 변환이 모두 포함된 것이다.

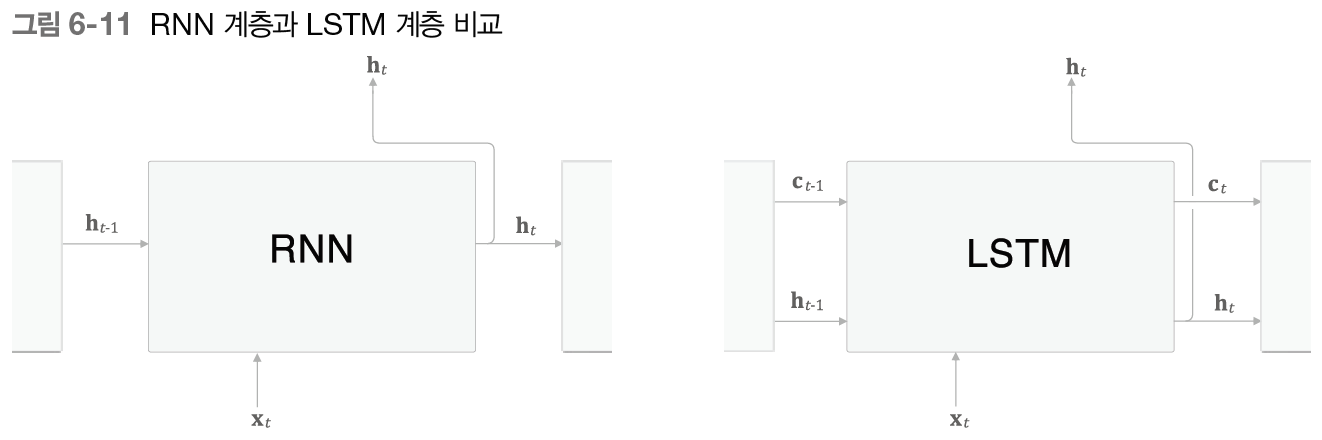
위의 그림에서 보듯이, LSTM 계층의 인터페이스에는 c라는 경로가 있다는 차이가 있다. c는 '기억 셀'이라 하며, LSTM 전용의 기억 메커니즘이다. 기억 셀의 특징은 데이터를 자기 자신으로만 주고받는다는 것이다. 즉, LSTM 계층 내에서만 완결되고, 다른 계층으로는 출력하지 않는다. 반면, LSTM의 은닉 상태 h는 RNN 계층과 마찬가지로 다른 계층으로 출력된다.

LSTM 계층 조립하기

LSTM의 기억 셀 C(t)에는 시각 t에서의 LSTM의 기억이 저장돼 있는데, 과거로부터 시각 t까지에 필요한 모든 정보가 저장돼 있다고 가정한다. 그리고 필요한 정보를 모두 간직한 이 기억을 바탕으로, 외부 계층에 은닉 상태 H(t)를 출력한다. 이때 출력하는 H(t)는 아래 그림과 같이 기억 셀의 값을 tanh 함수로 변환한 값이다.

위의 그림처럼 현재의 기억 셀 C(t)는 3개의 입력으로부터 '어떤 계산'을 수행하여 구할 수 있다. 여기서 핵심은 갱신된 C(t)를 사용해 은닉 상태 H(t)를 계산한다는 것이다. 또한 이 계산은 H(t) = tanh(C(t))인데, 이는 C(t)의 각 요소에 tanh 함수를 적용한다는 뜻이다.

'게이트'라는 것에 대해 알아볼 것이다. 게이트는 데이터의 흐름을 제어한다.

LSTM에서 사용하는 게이트는 다음 단계로 흘려보낼 물의 양을 제어한다.

output 게이트

tanh(C(t))에 게이트를 적용하는 걸 생각해보자. tanh(C(t))의 각 원소에 대해 '그것이 다음 시각의 은닉 상태에 얼마나 중요한가'를 조정한다. 이 게이트는 다음 은닉 상태 H(t)의 출력을 담당하는 게이트이므로 output 게이트(출력 게이트)라고 한다.

output 게이트의 열림 상태는 입력 X(t)와 이전 상태 H(t-1)로부터 구한다. 이때의 계산은 위의 식과 같다. 여기서 사용하는 가중치 매개변수와 편향에는 output의 첫 글자인 o를 첨자로 추가한다. 시그모이드 함수는 σ()로 표기한다.

위의 식에서 보면, 입력 X(t)에는 가중치 W(x(o))가 있고, 이전 시각의 은닉 상태 H(t-1)에는 가중치 W(h(o))가 붙어있다. 그리고 이 행렬들을 곱과 편향 B(o)를 모두 더한 다음 시그모이드 함수를 거쳐 출력 게이트의 출력 o를 구한다. 마지막으로 이 o와 tanh(C(t))의 원소별 곱을 H(t)로 출력하는 것이다.

그리고 σ의 출력을 o라고 하면 H(t)는 o와 tanh(C(t))의 곱으로 계산한다. 여기서 말하는 '곱'이란 원소별 곱이며, 이것을 아다마르 곱이라고도 한다. 아마다르 곱을 기호로는 ⊙으로 나타낸다.

이상이 LSTM의 output 게이트이다.

tanh의 출력은 -1.0 ~ 1.0의 실수이다. 이 -1.0 ~ 1.0의 수치를 그 안에 인코딩된 '정보'의 강약을 표시한다고 해석할 수 있다. 한편 시그모이드 함수의 출력은 0.0 ~ 1.0의 실수이며, 데이터를 얼마만큼 통과시킬지를 정하는 비율을 뜻한다. 따라서 게이트에서는 시그모이드 함수가, 실질적인 '정보'를 지니는 데이터에는 tanh 함수가 활성화 함수로 사용된다.

forget 게이트

C(t-1)의 기억 중에서 불필요한 기억을 잊게 해주는 게이트를 추가할 것이다. 이를 forget 게이트라 부를 것이다.

forget 게이트를 LSTM 계층에 추가하면 계산 그래프가 아래 그림처럼 된다.

위의 그림에서 forget 게이트가 수행하는 일련의 계산을 σ 노드로 표기했다. 이 σ 안에는 forget 게이트 전용의 가중치 매개변수가 있으며, 아래의 식으로 수행한다.

forget 게이트의 출력 f가 구해진다. 그리고 이 f와 이전 기억 셀인 C(t-1)과의 원소별 곱, 즉 C(t) = f⊙C(t-1)을 계산하여 C(t)를 구한다.

새로운 기억 셀

forget 게이트를 거치면서 이전 시각의 기억 셀로부터 잊어야 할 기억이 삭제되었다. 새로 기억해야 할 정보를 기억 셀에 추가해야 한다. 아래 그림과 같이 tanh 노드를 추가한다.

위에 그림에서 보듯이, tanh 노드가 계산한 결과가 이전 시각의 기억 셀 C(t-1)에 더해진다. 기억 셀에 새로운 '정보'가 추가된 것이다. 이 tanh 노드는 '게이트'가 아니며, 새로운 '정보'를 기억 셀에 추가하는 것이 목적이다. 따라서 활성화 함수로는 시그모이드 함수가 아닌 tanh 함수가 사용된다. tanh 노드에서 수행하는 계산은 다음과 같다.

기억 셀에 추가하는 새로운 기억을 g로 표기했다. 이 g가 이전 시각의 기억 셀인 C(t-1)에 더해짐으로써 새로운 기억이 생겨난다.

iunput 게이트

g에 게이트를 하나 추가할 것이다. 새롭게 추가하는 게이트를 input 게이트라고 할 것이다. input 게이트를 추가하면 계사 그래프가 아래 그림처럼 변한다.

input 게이트는 g의 각 원소가 새로 추가되는 정보로써의 가치가 얼마나 큰지를 판단한다. 새 정보를 무비판적으로 수용하는 게 아니라, 적절히 취사선택하는 것이 이 게이트의 역할이다. 다른 관점에서 보면, input 게이트에 의해 가중된 정보가 새로 추가되는 셈이다. input 게이트를 σ로, 그 출력을 i로 표기한다. 이때 수행하는 계산은 다음과 같다.

이 다음 i와 g의 원소별 곱 결과를 기억 셀에 추가한다.

LSTM의 기울기 흐름

기억 셀에만 집중하여, 그 역전파의 흐름을 그린 것이다. 이때 기억 셀의 역전파에서는 '+'와 'x' 노드만을 지나게 된다. '+' 노드는 상류에서 전해지는 기울기를 그대로 흘리기만 한다. 따라서 기울기 변화는 일어나지 않는다.

'x' 노드는 '행렬 곱'이 아닌 '원소별 곱(아마다르 곱)'을 계산한다. 매 시각 다른 게이트 값을 이용해 원소별 곱을 계산한다. 이처럼 매번 새로운 게이트 값을 이용하므로 곱셈의 효과가 누적되지 않아 기울기 소실이 일어나지 않는 것이다.

위 그림에서 'x' 노드의 계산은 forget 게이트가 제어한다. 그리고 forget 게이트가 '잊어서는 안 된다'라고 판단한 원소에 대해서는 그 기울기가 약화되지 않은 채로 과거 방향으로 전해진다. 따라서 기억 셀의 기울기가 소실 없이 전파되리라 기대할 수 있다.

LSTM 구현

최초의 한 단계만 처리하는 LSTM 클래스를 구현한 다음, 이어서 T개의 단계를 한꺼번에 처리하는 Time LSTM 클래스를 구현할 것이다.

4개의 가중치를 하나로 모을 수 있고, 그렇게 하면 원래 개별적으로 총 4번을 수행하던 아핀 변환을 단 1회의 계산으로 끝마칠 수 있다. 계산 속도가 빨라진다는 뜻이다. W(x), W(h), B 각각에 4개분의 가중치가 포함되어 있다고 가정하고, 이때의 LSTM을 계산 그래프로 그려보면 아래 그림과 같이 된다.

여기에서는 처음 4개분의 아핀 변환을 한꺼번에 수행한다. 그리고 slice 노드를 통해 그 4개의 결과를 꺼낸다. slice는 아핀 변환의 결과를 균등하게 4조각으로 나눠서 꺼내 주는 단순한 노드이다. slice 노드 다음에는 활성화 함수(시그모이드 또는 tanh 함수)를 거쳐 계산이 이루어진다.

class LSTM:
    def __init__(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None

초기화 인수는 가중치 매개변수인 Wx와 Wh, 그리고 편향을 뜻하는 b이다. 이 가중치에는 4개분의 가중치가 담겨 있다. 이 인수들을 인스턴스 변수인 params에 할당하고, 이에 대응하는 형태로 기울기도 초기화한다. cache는 순전파때 중간 결과를 보관했다가 역전파 계산에 사용하려는 용도의 인스턴스 변수이다.

다음으로 순전파 구현을 살펴보자.

def forward(self, x, h_prev, c_prev):
        Wx, Wh, b = self.params
        N, H = h_prev.shape
        
        A = np.matmul(x, Wx) + np.matmul(h_prev, Wh) + b
        
        # slice
        f = A[:, :H]
        g = A[:, H:2*H]
        i = A[:, 2*H:3*H]
        o = A[:, 3*H:]
        
        f = sigmoid(f)
        g = np.tanh(g)
        i = sigmoid(i)
        o = sigmoid(o)
        
        c_next = f * c_prev + g * i
        h_next = o * np.tanh(c_next)
        
        self.cache = (x, h_prev, c_prev, i, f, g, o, c_next)
        return h_next, c_next

이 메서드에서는 가장 먼저 아핀 변환을 한다.

미니배치 수를 N, 입력 데이터의 차원 수를 D, 기억 셀과 은닉 상태의 차원 수를 모두 H로 표시했다. 그리고 계산 결과인 A에는 네 개분의 아핀 변환 결과가 저장된다. 따라서 이 결과로부터 데이터를 꺼낼 때는 A[:, :H]나 A[:, H:2*H] 형태로 슬라이스해서 꺼내고, 꺼낸 데이터를 다음 연산 노드에 분배한다.

LSTM의 역전파는 계산 그래프를 역방향으로 전파해 구할 수 있다.

저작자표시 동일조건